Use the definition of a logarithm to solve logarithmic equations
We have already seen that every logarithmic equation is equivalent to the exponential equation . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation . To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x:
A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations
For any algebraic expression S and real numbers b and c, where ,
Example 9: Using Algebra to Solve a Logarithmic Equation
Solve .
Solution
Try It 9
Solve .
SolutionExample 10: Using Algebra Before and After Using the Definition of the Natural Logarithm
Solve .
Solution
Try It 10
Solve .
SolutionExample 11: Using a Graph to Understand the Solution to a Logarithmic Equation
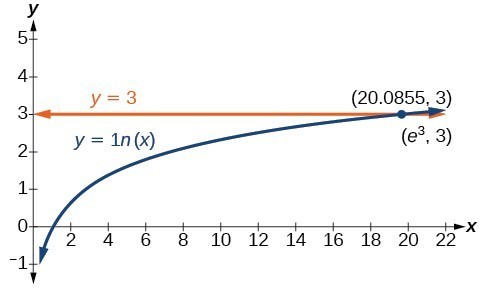
Solve .
Solution
Figure 2 represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words . A calculator gives a better approximation: .
Try It 11
Use a graphing calculator to estimate the approximate solution to the logarithmic equation to 2 decimal places.
Solution